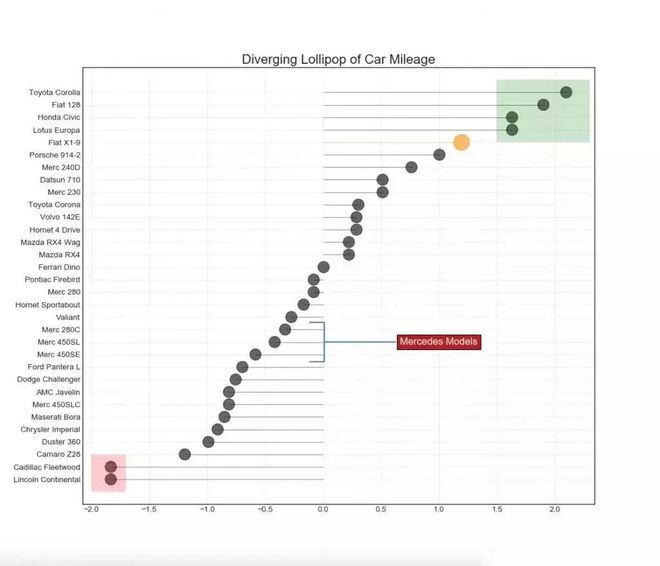
带标记的棒棒糖图通过强调您想要引起注意的任何重要数据点并在图表中适当地给出推理，提供了一种对差异进行可视化的灵活方式。

　　人口金字塔可用于显示由数量排序的组的分布。 或者它也可以用于显示人口的逐级过滤，因为它在下面用于显示有多少人通过营销渠道的每个阶段◆◆◆。

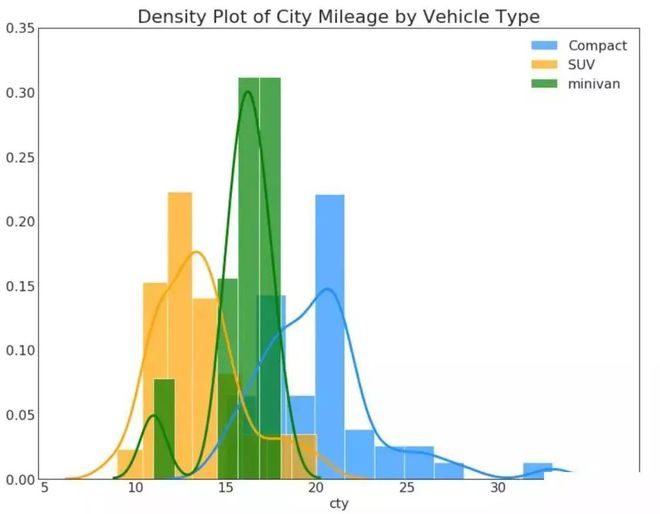
　　带有直方图的密度曲线汇集了两个图所传达的集体信息◆■★★，因此您可以将它们放在一个图中而不是两个图中■★★■★。

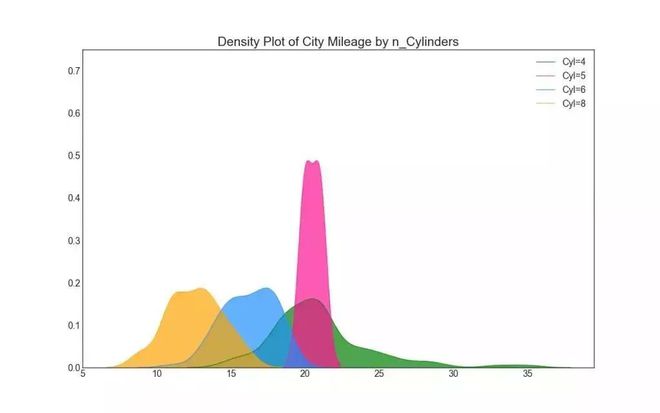
　　密度图是一种常用工具◆★，用于可视化连续变量的分布。 通过“响应◆■■◆★★”变量对它们进行分组，您可以检查 X 和 Y 之间的关系。 以下情况用于表示目的，以描述城市里程的分布如何随着汽缸数的变化而变化。

　　美国顶流科技大厂超爱的大学 Top 10！本科毕业后年薪百万都算少的..■★◆★★◆.◆★..

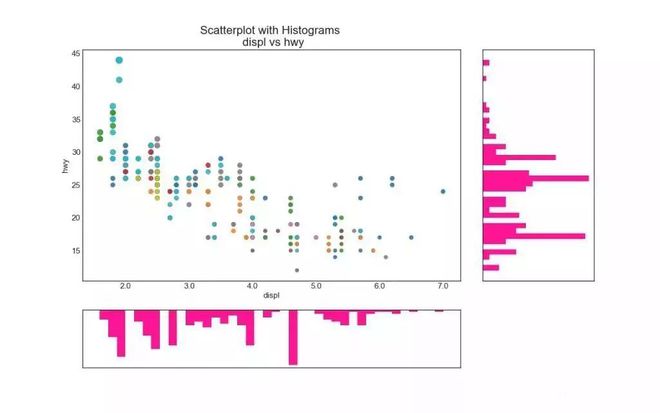
　　边缘直方图具有沿 X 和 Y 轴变量的直方图。 这用于可视化 X 和 Y 之间的关系以及单独的 X 和 Y 的单变量分布。 这种图经常用于探索性数据分析(EDA)。

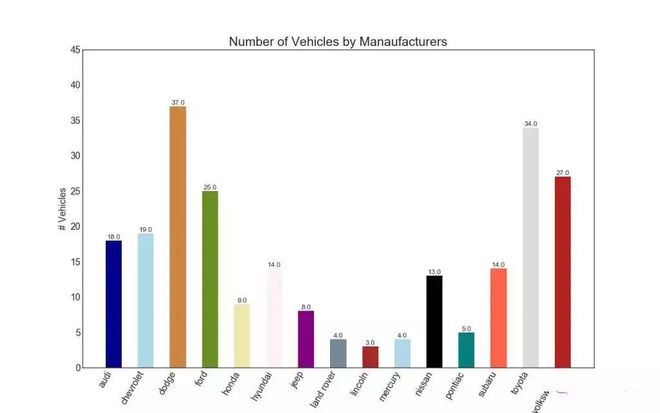
　　条形图是基于计数或任何给定指标可视化项目的经典方式◆■。 在下面的图表中，我为每个项目使用了不同的颜色，但您通常可能希望为所有项目选择一种颜色，除非您按组对其进行着色◆◆★。

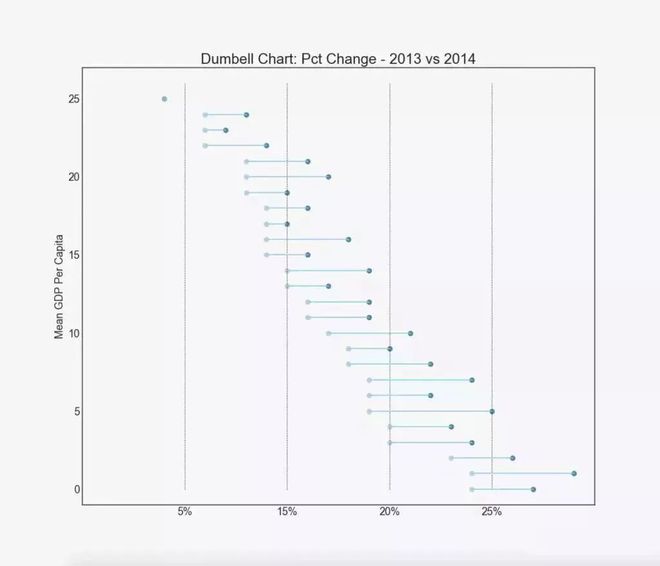
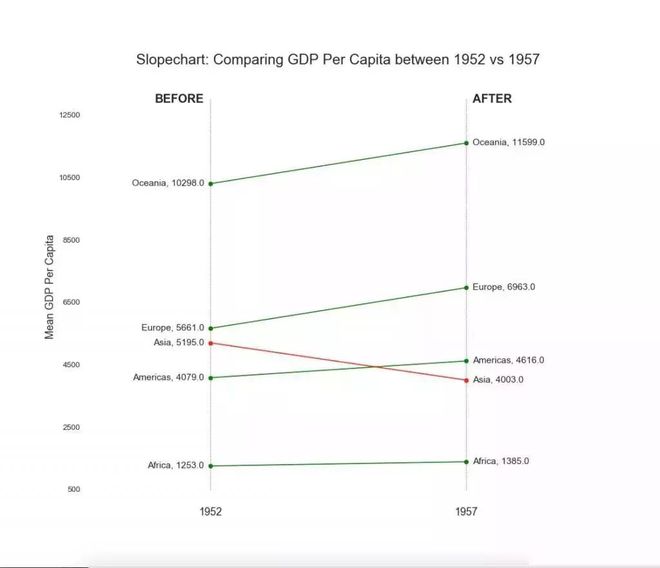
　　哑铃图表传达了各种项目的“前”和“后”位置以及项目的等级排序。 如果您想要将特定项目/计划对不同对象的影响可视化★■◆，那么它非常有用。

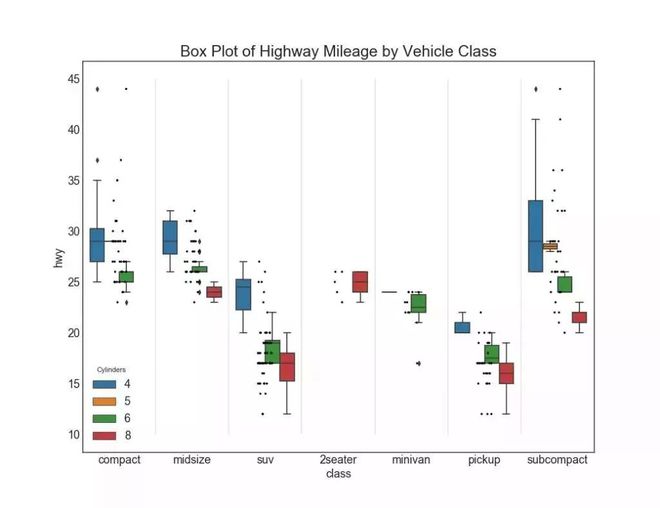
　　箱形图是一种可视化分布的好方法，记住中位数■◆、第25个第45个四分位数和异常值。 但是，您需要注意解释可能会扭曲该组中包含的点数的框的大小。 因此，手动提供每个框中的观察数量可以帮助克服这个缺点。

　　■★◆“东北雨姐■◆◆★”卖的红薯粉果然没一点红薯！10多天掉粉186万■★◆■，厂家曾称只掺了三分之一的木薯

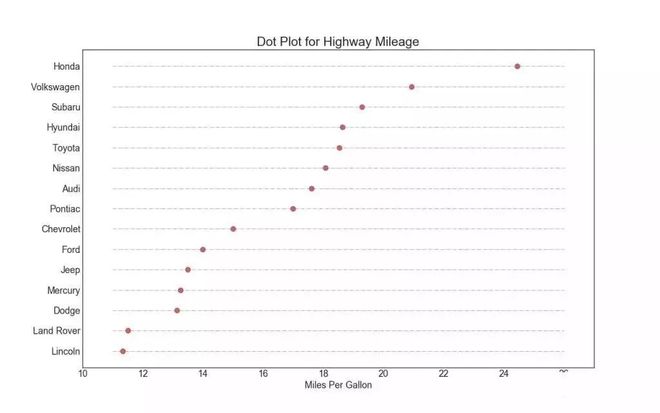
　　包点图表传达了项目的排名顺序，并且由于它沿水平轴对齐★★◆■★■，因此您可以更容易地看到点彼此之间的距离★■◆。

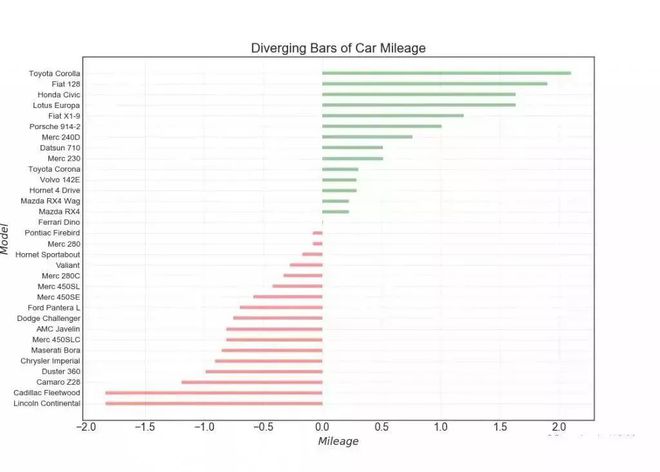
　　如果您想根据单个指标查看项目的变化情况，并可视化此差异的顺序和数量，那么散型条形图 (Diverging Bars) 是一个很好的工具◆★■★★◆。 它有助于快速区分数据中组的性能，并且非常直观■■◆★★★，并且可以立即传达这一点◆★★★。

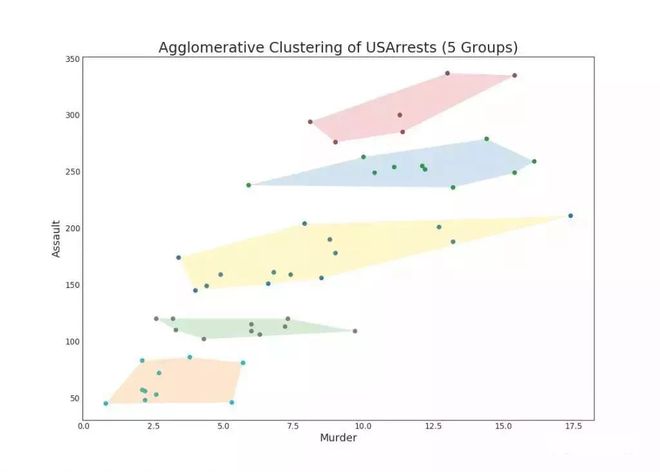
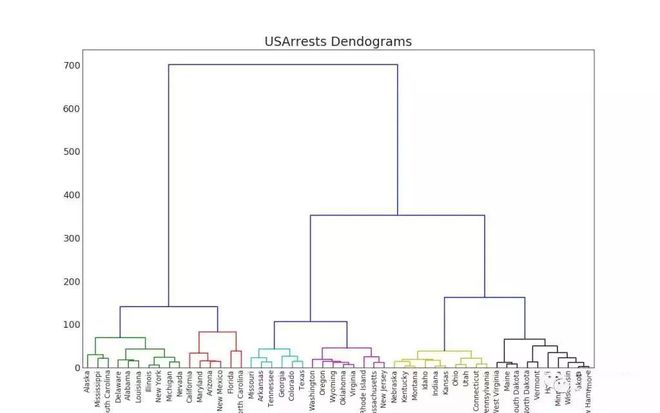
　　簇状图 (Cluster Plot)可用于划分属于同一群集的点。 下面是根据USArrests数据集将美国各州分为5组的代表性示例◆◆★■★。 此图使用■★◆◆★■“谋杀”和“攻击”列作为X和Y轴。 或者，您可以将第一个到主要组件用作X轴和Y轴。

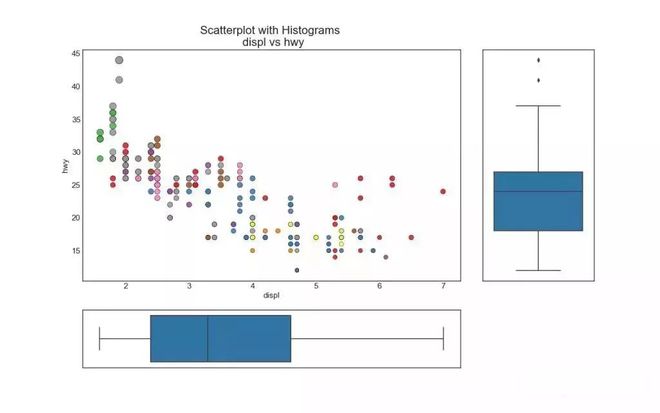
　　边缘箱图与边缘直方图具有相似的用途◆★■。 然而，箱线图有助于精确定位 X 和 Y 的中位数、第25和第75百分位数。

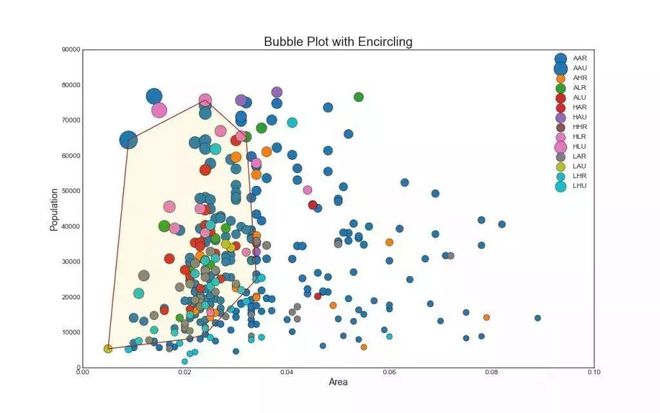
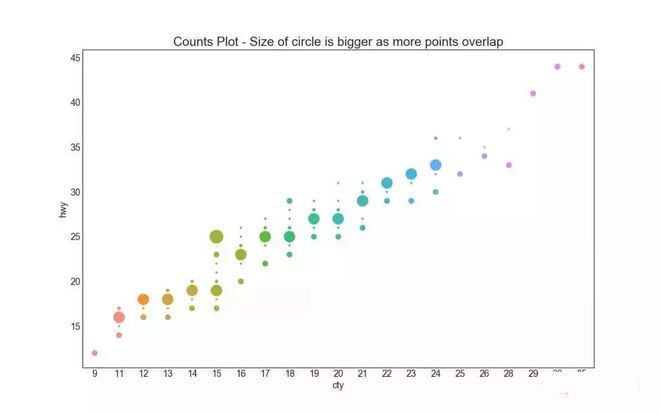
　　避免点重叠问题的另一个选择是增加点的大小，这取决于该点中有多少点。 因此，点的大小越大，其周围的点的集中度越高。

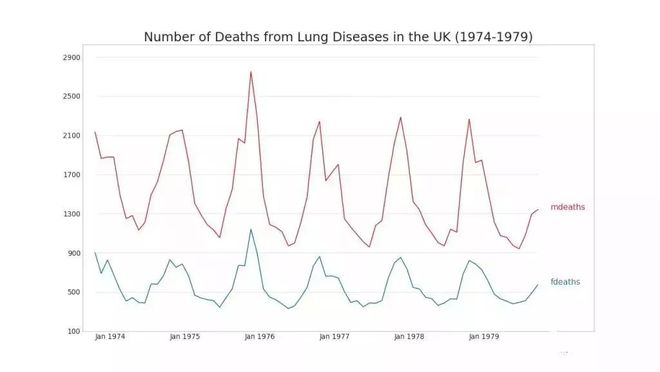
　　如果要显示在同一时间点测量两个不同数量的两个时间序列★■◆◆★，则可以在右侧的辅助Y轴上再绘制第二个系列。

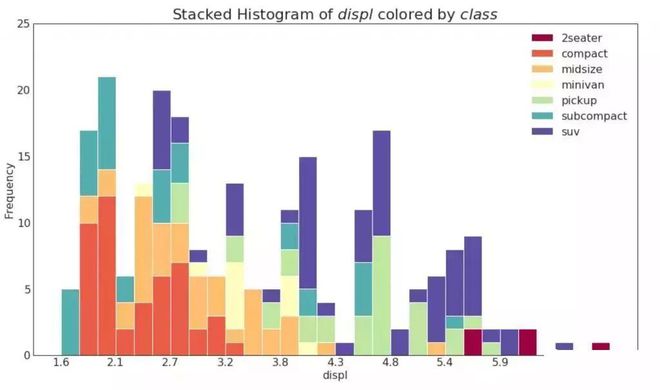
　　直方图显示给定变量的频率分布。 下面的图表示基于类型变量对频率条进行分组，从而更好地了解连续变量和类型变量。

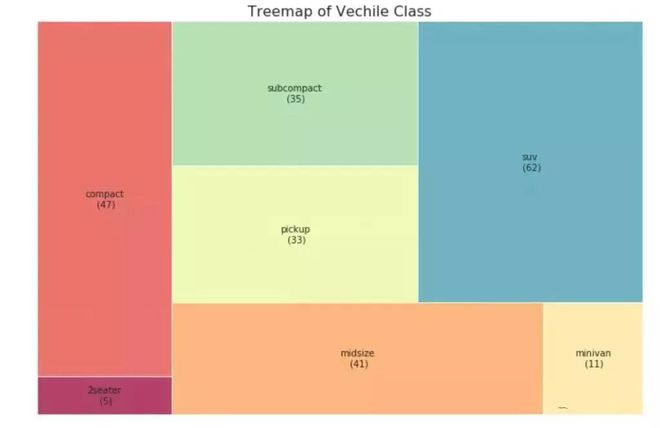
　　树形图基于给定的距离度量将相似的点组合在一起，并基于点的相似性将它们组织在树状链接中。

　　对于空乘旅客■■，我们看到多达14个滞后跨越蓝线◆★★■★，因此非常重要◆★◆★■★。 这意味着，14年前的航空旅客交通量对今天的交通状况有影响。

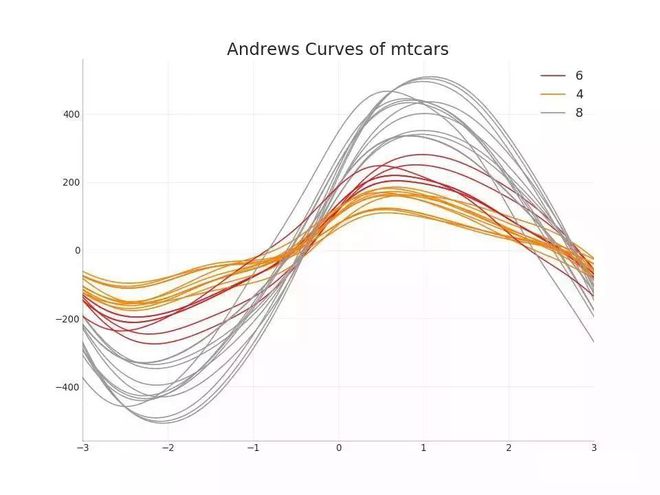
　　安德鲁斯曲线有助于可视化是否存在基于给定分组的数字特征的固有分组。 如果要素(数据集中的列)无法区分组(cyl)，那么这些线将不会很好地隔离■■★◆，如下所示。

　　与时间序列相比，日历地图是可视化基于时间的数据的备选和不太优选的选项。 虽然可以在视觉上吸引人，但数值并不十分明显。 然而■■■★★★，它可以很好地描绘极端值和假日效果。

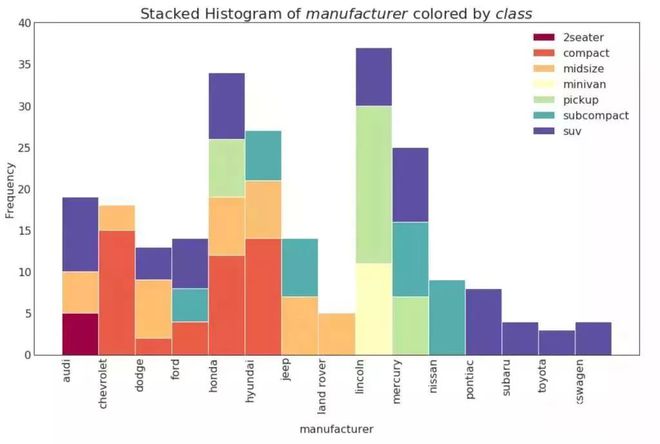
　　类型变量的直方图显示该变量的频率分布◆■★。 通过对条形图进行着色，可以将分布与表示颜色的另一个类型变量相关联。

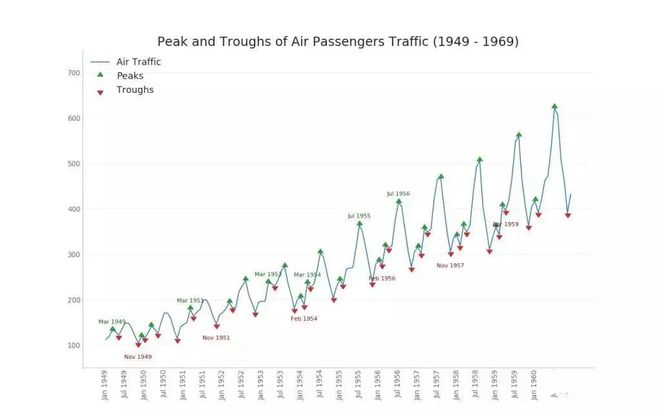
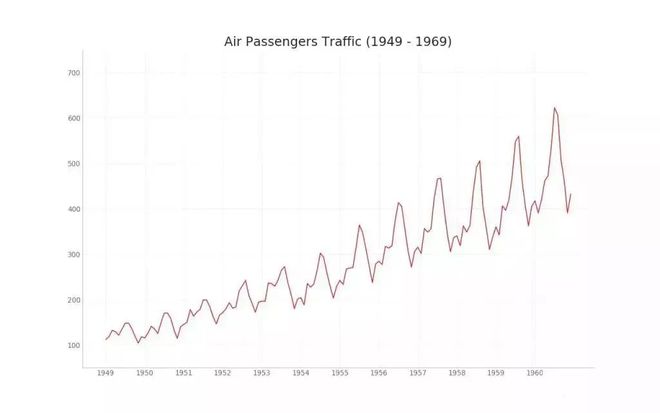
　　时间序列图用于显示给定度量随时间变化的方式。 在这里，您可以看到 1949年 至 1969年间航空客运量的变化情况★◆★◆■。

　　相关图用于直观地查看给定数据框(或二维数组)中所有可能的数值变量对之间的相关度量★■★★■。

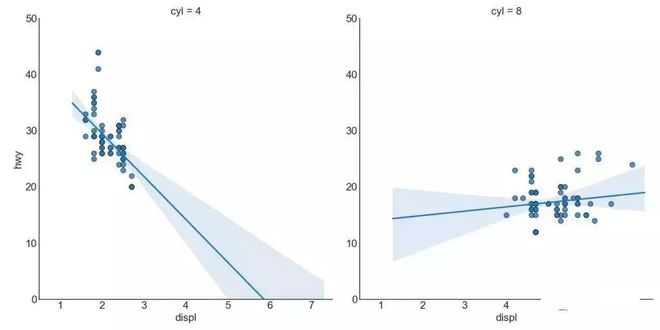
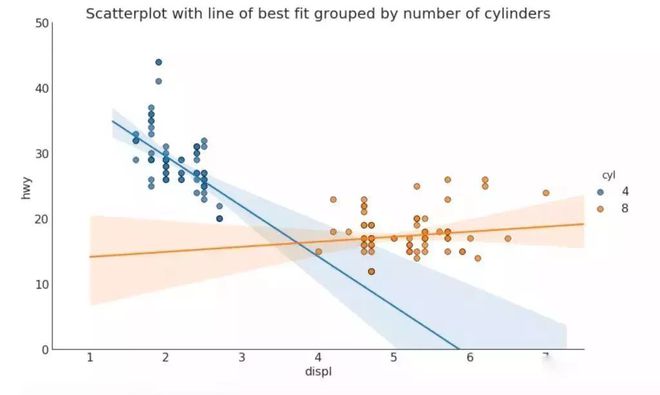
　　如果你想了解两个变量如何相互改变，那么最佳拟合线就是常用的方法。 下图显示了数据中各组之间最佳拟合线的差异。

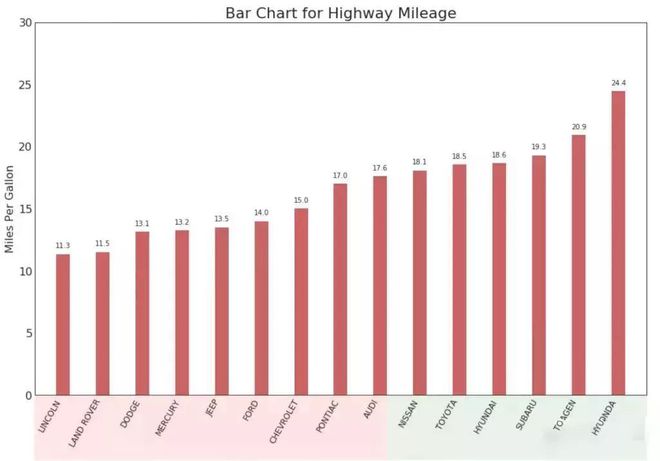
　　有序条形图有效地传达了项目的排名顺序■★■■。 但是■★★★，在图表上方添加度量标准的值，用户可以从图表本身获取精确信息。

　　饼图是显示组成的经典方式。 然而，现在通常不建议使用它，因为馅饼部分的面积有时会变得误导。 因此，如果您要使用饼图，强烈建议明确记下饼图每个部分的百分比或数字★◆■■★。

　　如果您有一个时间序列数据集，每个时间点(日期/时间戳)有多个观测值，则可以构建带有误差带的时间序列。 您可以在下面看到一些基于每天不同时间订单的示例。 另一个关于45天持续到达的订单数量的例子◆★◆★。

　　未堆积面积图用于可视化两个或更多个系列相对于彼此的进度(起伏)。 在下面的图表中，您可以清楚地看到随着失业中位数持续时间的增加，个人储蓄率会下降。 未堆积面积图表很好地展示了这种现象。

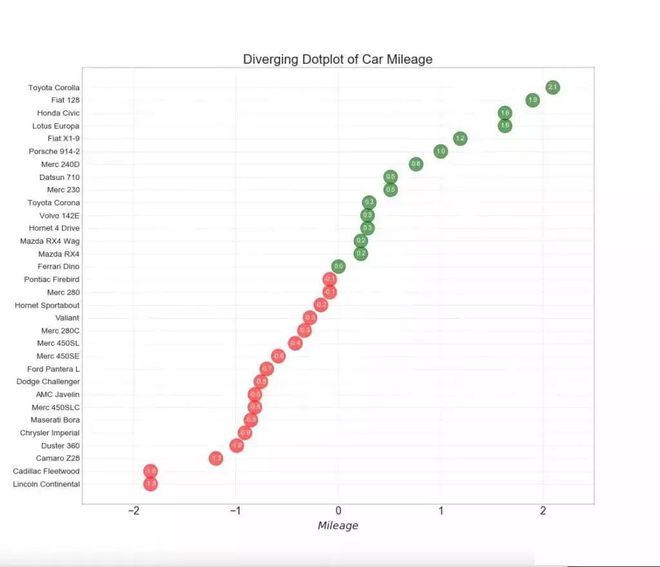
　　发散型包点图 (Diverging Dot Plot)也类似于发散型条形图 (Diverging Bars)。 然而，与发散型条形图 (Diverging Bars)相比■★■■，条的缺失减少了组之间的对比度和差异■◆★◆◆★。

　　小提琴图是箱形图在视觉上令人愉悦的替代品◆◆。 小提琴的形状或面积取决于它所持有的观察次数。 但是■■◆◆★，小提琴图可能更难以阅读■■★■◆，并且在专业设置中不常用。

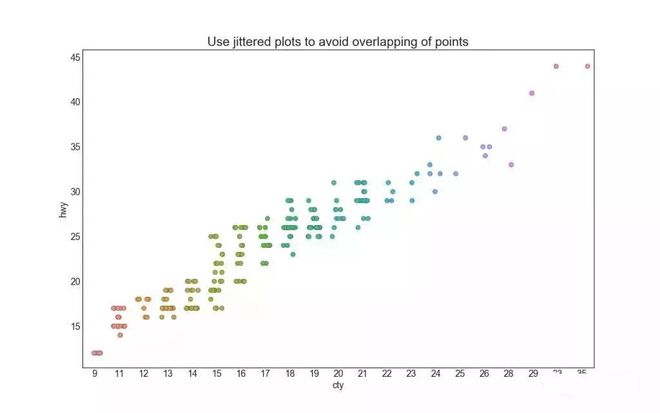
　　通常■◆◆◆，多个数据点具有完全相同的 X 和 Y 值。 结果，多个点绘制会重叠并隐藏。 为避免这种情况，请将数据点稍微抖动，以便您可以直观地看到它们■★■■■。

　　矩阵图是探索性分析中的最爱，用于理解所有可能的数值变量对之间的关系。 它是双变量分析的必备工具。

　　《编码物候》展览开幕 北京时代美术馆以科学艺术解读数字与生物交织的宇宙节律

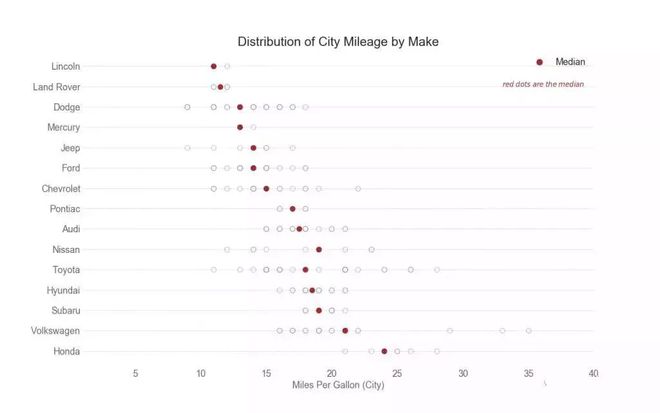
　　分布式包点图显示按组分割的点的单变量分布★★◆。 点数越暗，该区域的数据点集中度越高。 通过对中位数进行不同着色，组的真实定位立即变得明显。

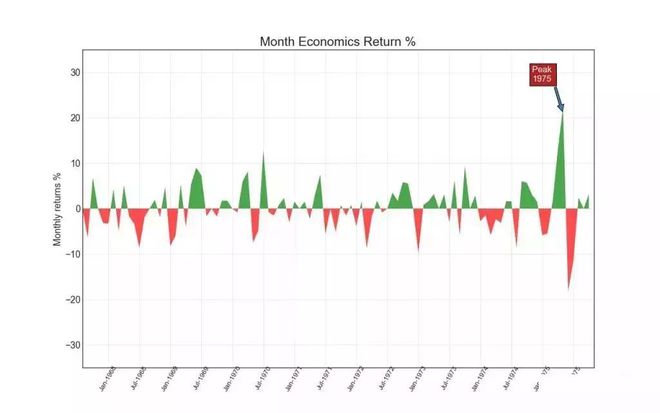
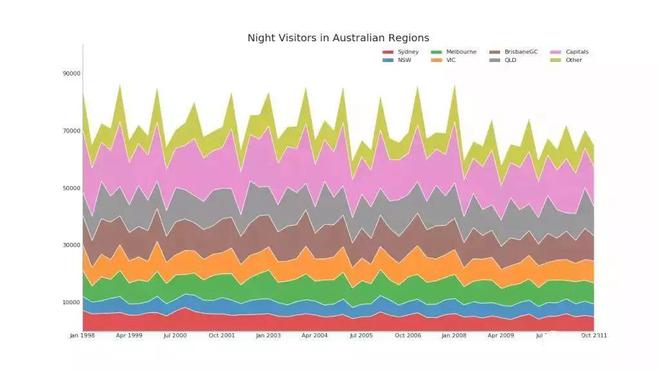
　　通过对轴和线之间的区域进行着色，面积图不仅强调峰和谷◆■★■★★，而且还强调高点和低点的持续时间。 高点持续时间越长，线下面积越大■★★★◆■。

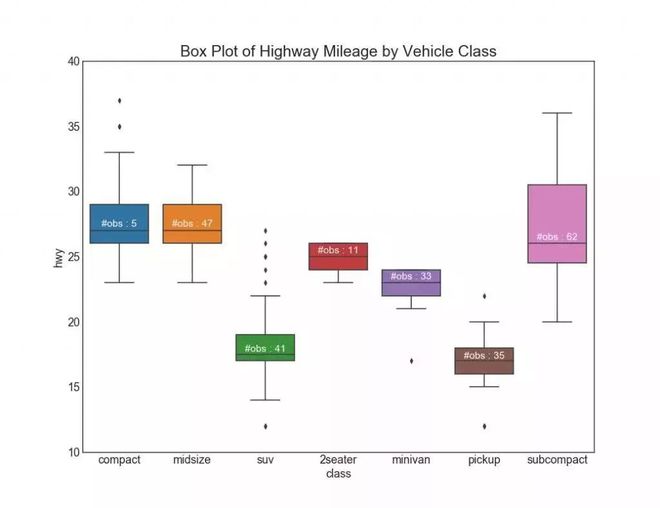
　　包点+箱形图 (Dot + Box Plot)传达类似于分组的箱形图信息◆★★■。 此外■■，这些点可以了解每组中有多少数据点。

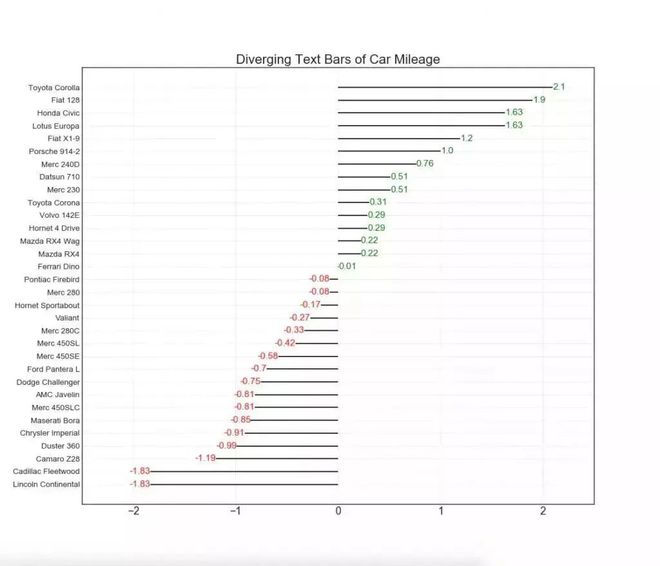
　　发散型文本 (Diverging Texts)与发散型条形图 (Diverging Bars)相似■★■■■◆，如果你想以一种漂亮和可呈现的方式显示图表中每个项目的价值，就可以使用这种方法。

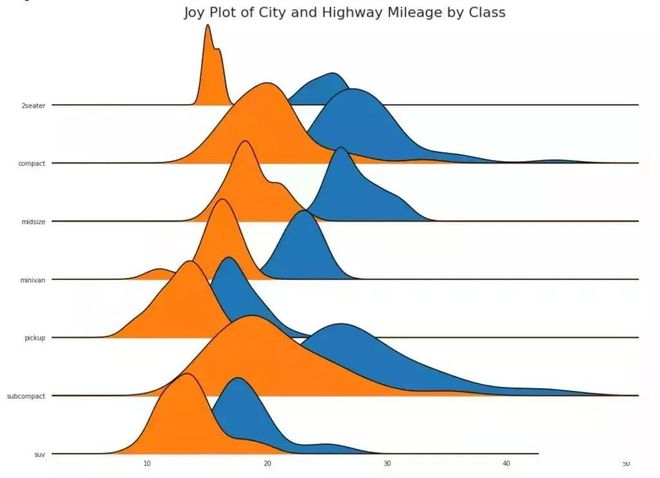
　　Joy Plot允许不同组的密度曲线重叠，这是一种可视化大量分组数据的彼此关系分布的好方法。 它看起来很悦目，并清楚地传达了正确的信息。

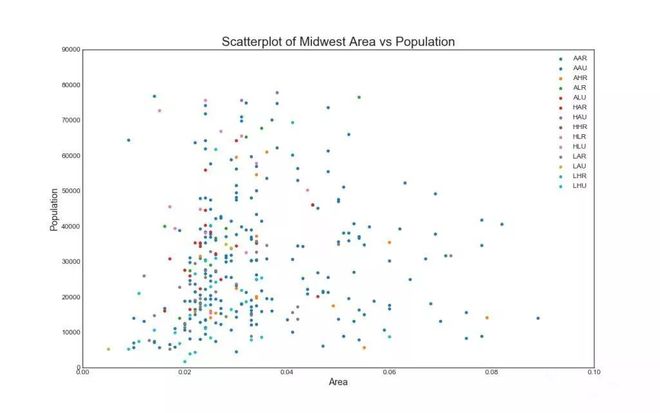
　　散点图是用于研究两个变量之间关系的经典的和基本的图表。 如果数据中有多个组，则可能需要以不同颜色可视化每个组。

　　PACF在另一方面显示了任何给定滞后(时间序列)与当前序列的自相关，但是删除了滞后的贡献。

　　自相关图(ACF图)显示时间序列与其自身滞后的相关性。 每条垂直线(在自相关图上)表示系列与滞后0之间的滞后之间的相关性★◆◆。 图中的蓝色阴影区域是显着性水平。 那些位于蓝线之上的滞后是显着的滞后。

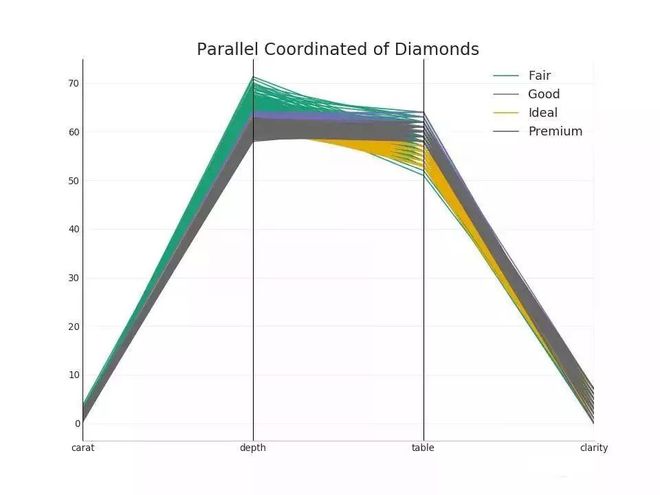
　　平行坐标有助于可视化特征是否有助于有效地隔离组。 如果实现隔离，则该特征可能在预测该组时非常有用。

　　ROG Z890吹雪主板在京东先人一步首发 晒单返100元E卡可享6期免息

　　）所推送文章中★★◆■■，部分来源于网络。除非确实无法确认■◆★■★，我们都会注明作者和来源■◆。部分文章推送时未能与原作者取得联系★◆★■。若涉及版权问题★◆◆◆，烦请原作者联系我们，我们会在24小时内删除处理，谢谢！内容若有误■★◆★◆，欢迎批评指正